1. la transmission
électromagnétique
Elle fait appel à :
·
un médium guidé (Guided medium) : paires
torsadées, câbles coaxial,
·
un médium non guide (Unguided medium):
air dans le cas de la radio
transmission, communication par satellite
2. la transmission optique
Dans
ce cas le medium est la fibre optique.
DOMAINES FREQUENTIELS:
LES SUPPORTS UTILISES :
·
Les
paires filaires torsadées
·
Peu
couteux
·
Facile
à déployer
·
Bande
passante limitée
·
Perte
élevées
·
Le
câble coaxial
·
Bande
passante limitée
·
Pertes
faibles
·
Plus
couteux que les paires torsadées
·
Les
faisceaux hertziens
·
Propagation
linéaire (visibilité) en HF
·
Spectre
limité (bande passante limitée)
·
Les fibres optiques
·
Pertes
faibles
·
Bande
passante élevée
·
Immunité
aux bruits
·
Mise
en œuvre délicate et couteuse
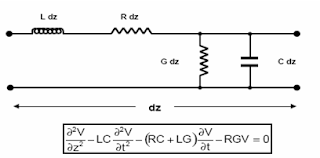
MODELISATION D’UNE LIGNE DE COMMUNICATION SUR SUPPORT METALLIQUE
1
Modélisation d'une ligne :
Une
ligne de communication sur support métallique peut être modélisée par une
succession de tronçons élémentaires de longueur dz (voir figue 2.1), assimilés
à des quadripôles élémentaires composés des paramètres r, l, g, c, avec :
R : résistance Ohms/m
L : inductance H/m
G :
conductance (fuite des isolants ou fuite entre conducteurs) Ohms/m.
C :
capacité entre les conducteurs F/m
2 L'équation des télégraphistes
Cette équation permet de calculer le courant et la tension en tout
point d'une ligne
Modélisation d’une ligne de transmission sur support
métallique
Dans le cas d'une ligne infinie et d'un générateur sinusoïdal
l’expression de la tension V(z) est donc la combinaison d'une atténuation et
d'un déphasage
e-αz représente
le terme d’atténuation
e-jβz représente le terme de déphasage.
Autre
formulation avec un tronçon unitaire dx=1
Modélisation d’une ligne de transmission sur
support métallique
La
tension dans ce tronçon élémentaire dx est donnée par l’équation 2.1
Le courant circulant dans cette portion est :
(2.2)
Dérivons l’équation 2.1
( 2.3)
Nous
obtenons une équation différentielle de la forme
u’’(x)-δ2u(x)=0 (2.4)
Avec δ2=(R+jLw)(G+jCw). (2.5)
δ
étant le coefficient de propagation.
Avec α : atténuation (en Neper/m)
β : propagation (en rd/m)
la vitesse de propagation sera alors v=w/β
La
solution de l’équation (5) donne une expression de u(x) se présentant comme la
somme d’une onde incidente et une onde réfléchie.
Nous
pouvons définir l’impédance caractéristique
(Ω) (2.9)
Dans
le cas d’une ligne sans perte (R=G=0) alors
4.3
Taux d’Onde Stationnaire et Coefficient de Réflexion
Pour
un câble d'impédance Zc fermé sur une impédance Zt on définit :
Le
taux d'ondes stationnaires : TOS
Le
coefficient de réflexion : k
Cas
particuliers
·
Zt=0 (court-circuit), TOS=0 et
k=-1 : réflexion totale avec inversion
·
Zt=∞ (ouvert), TOS=∞ et k=1 :
réflexion totale
·
Zt=Zc (adaptation), TOS=1 et k=0
: onde incidente totalement absorbée
Exemple
·
Zc=50Ω, Zt=75Ω, TOS=1.5 et k=0.2 : soit une réflexion
de 20% de l'onde incidente.
En
transmission de données, le temps de propagation ne sera pas négligeable devant
la longueur d’onde du signal, il sera donc nécessaire d’assurer une adaptation
aux extrémités du câble afin d’éviter un écho perturbant.
Si
on doit raccorder deux impédances différentes, il faut utiliser un
transformateur d’impédance (pertes très faibles).
4.4
Résistance :
L'atténuation
d'une ligne dépend essentiellement de R (pertes joules), R dépend :
·
de la résistivité du matériau
(généralement du cuivre dont ñ = 1.65 10-8 Ω.m à
1.85
10-8 Ωm selon la
composition, habituellement 1.7 10-8 Ω.m).
·
de la section (R=rl/s).
·
de la température.
·
de la fréquence (effet pelliculaire).
4.5
Effet de la température
R=R0[1+a(T−T0)] avec a=3,93 10-3 /°C pour le
cuivre.
si
R à 20°C vaut 1kΩ à 50°C R devient 1.118 kΩ
4.6
Effet pelliculaire
Dans
le cas du courant alternatif, la densité de courant dans la section du conducteur
n'est pas constante (phénomène électromagnétique). Le courant se
répartitexponentiellement de la surface vers l'intérieur.
Pour
une densité de 1 à la surface, celle ci est de 1/e à une distance d .
On
considère que l'épaisseur utile est définie par d (si d << rayon).
exemples
(câbles cuivre) :
f=50Hz
, d = 9.3mm
f=10MHz,
d
= 20 μm

















No comments:
Post a Comment